
| Uni Jena |
| PH Erfurt |
| Vorlesungen |
| Veröffentlichungen |
| Studentenarbeiten |
| TAURUS |
| CHARM |
| TU Ilmenau |
Astronomieprogramm TAURUS
Das Programm TAURUS dient der Auswertung von astronomischen Beobachtungen. Es eignet sich für Amateurastronomen und für astonomische Praktika in Schulen und Universitäten.
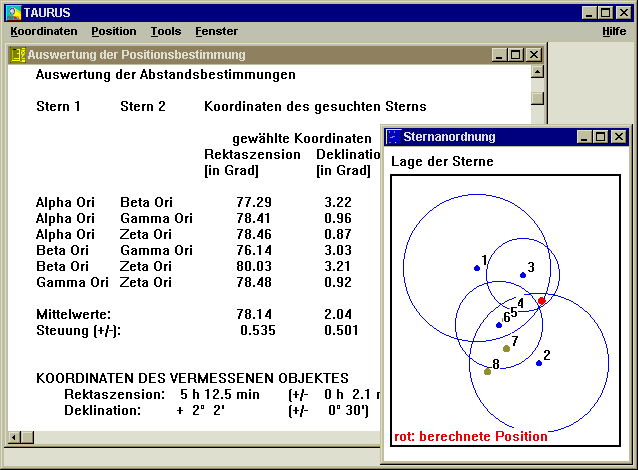
Bildschirmfoto aus dem Programm TAURUS
Das Programm ermöglicht die Umrechnung von Koordinaten der verschiedenen sphärischen Systeme ineinander, die Positionsbestimmung von Himmelskörpern aus Relativmessungen, die ungefähre Bestimmung des Abstandes eines Planetoiden von der Sonne und stellt weitere kleine Hilfsprogramme (Umrechnung von Winkeln, Sternzeitberechnung) bereit. Alle Programmteile sind unter einer Windows-Oberfläche vereinigt , so dass die Bedienung relativ einfach sein sollte.
Der erste Menü-Punkt KOORDINATEN ermöglicht die Umrechnung der Koordinaten folgender Systeme ineinander:
- Rotierendes äquatorsystem (Rektaszension, Deklination)
- Ruhendes äquatorsystem (Stundenwinkel, Deklination)
- Horizontsystem (Azimut, Höhe)
- Ekliptiksystem (ekliptikale Länge und Breite)
- Galaktisches System II (galaktische Länge und Breite)
Man wählt jeweils ein Koodinatensystem aus, in dem die Eingabe der Werte erfolgt und erhält in einem Fenster die Koordinatenangaben in allen fünf Systemen, wobei man vorher aufgefordert wird, Beobachtungszeit und -ort festzulegen. Zu diesem und den übrigen Punkten existieren editierbare Hilfetexte, die jeweils über den Punkt INFORMATION im Roll-up-Menü erreichbar sind.
Der umfangreichste Teil des Programms verbirgt sich hinter dem Menüpunkt POSITION. Dort kann mit Hilfe der in Artikel 1 (PDF, 33 KB) beschriebenen Methode die Position eines unbekannten Objektes berechnet werden, wenn man die Abstände zu benachbarten Referenzsternen kennt. Die Koordinaten von maximal acht Referenzsternen können als Datei gespeichert werden, um sie für künftige Auswertungen zur Verfügung zu haben. Die Auswertung erfolgt sowohl graphisch als auch in Form einer Tabelle. (siehe Abbildung)
Der Menüpunkt TOOLS stellt eine Reihe von kleineren Hilfsmitteln zur Verfügung. So kann man Koordinatenangaben (z.B. Rektaszension) vom Grad- ins Stundenmaß umrechnen und umgekehrt. Der Punkt WINKELABSTAND berechnet den Winkel zwischen zwei Objekten, deren Rektaszension und Deklination bekannt sind. Ein weiterer Menüpunkt berechnet die STERNZEIT für einen vorgegebenen Zeitpunkt und eine beliebige geographische Länge.
Der Punkt ABSTAND EINES PLANET(OID)EN ermöglicht die näherungsweise Berechnung des Abstandes eines Planetoiden von der Sonne aus je zwei Messungen der ekliptikalen Länge des Planetoiden und der Sonne. Die Berechnung beruht auf dem Verfahren, welches in Artikel 2 (PDF, 33 KB) beschrieben wurde.
Die Verfahren werden in der Hilfe zum Programm ausführlich erläutert. Dort finden Sie auch ein Glossar mit wichtigen Begriffen.
Das Programm ist nicht so komplex wie professionelle Software, bietet aber nach Meinung des Autors die wichtigsten Berechnungshilfsmittel an. Es kann frei weitergegeben werden, wobei der Nutzer über die Bibliothek der Dialogelemente im Borland-Stil BWCC.DLL verfügen muß, die er zusammen mit dem Programm erhält. Diese Bibliothek muß im gleichen Verzeichnis wie TAURUS.EXE oder im Windows-Verzeichnis stehen. Sie kann in Zusammenhang mit dem Programm ebenfalls weitergegeben werden.
Das Programm ist zwar auf CD-ROM erschienen. Interessenten können es aber auch downloaden. Das ZIP-Archiv hat eine Größe von 215 kB. [ Download ]
Berücksichtigen Sie bitte, dass das Programm aus dem Jahr 1994 stammt, und damit von seiner Oberfläche nicht mehr auf dem neusten Stand ist. Die Funktion sind jedoch weiterhin aktuell. Das Programm läuft auch unter den neuen Windows-Versionen.
Veröffentlichungen
- E. Schön, Eine Methode zur Positionsberechnung aus Relativmessungen, Die Sterne 70 (1994) 239-244 [PDF, 33 KB]
- E. Schön, Eine einfache Methode zur Bestimmung des Bahnradius eines Planetoiden, Die Sterne 70 (1994) 249-254 [PDF, 37 KB]
- E. Schön, TAURUS - Programm für astronomische Berechnungen, Die Sterne 71 (1995) 13-17
- CD-ROM Jupiter 2, Roth EDV 1995
Sitemap | Impressum | Datenschutzerklärung | Kontakt
© 1996-2023 Dr. Eckhardt Schön - Alle Rechte vorbehalten